Problems Plus

Putting these on a black background created the most brutal contrast... So here's an ugly greyish background

About the solutions: No, I'm not refering to myself in the 3rd person... I just mean 'we' as in me and you and whoever would want to solve the problem.

Here are quicklinks to completed ones, by the page # the problem was on: 089 201 393 536

Agh!  I just don't get it. Anyway, testing with a calculator gives 3/2 : )

Yeah.. I started this one, but it's boring.

The flaw is, of course, that each zero breaks into both a 1 and a -1, and in the fourth line, they only show the 1 not in a bracket.  They are 'forgetting' the -1 that goes at the end in the 5th line, that would return the answer to zero.  What a dumb problem..

089: Oooo..  This gets tricky if you don't handle it properly. Solution

BOOORing

Little does anyone suspect, everything else in the world is crooked, and this thing is level.

I hate problems like this...

Very cool problem.  I'll get to it soon. Well, that 'soon' translated as a whole year, but here it is!

OK.  Later, though.

Hmm...  I wish they'd specify whether you're supposed to use degrees, radians, or gradians!  I'll assume radians, and investigate later.

Hmm...  pattern-finding problem.  Ehhxcellent <tapping fingers together, Mr. Burns-like>

Zzzzz...

Hmm.. later, dude.

Interesting problem.  I'm thinking that there's one little leap of logic to make.  I'll see what change-of-base does to it.

393:  Cool.  See, the key to problem solving is that you don't need to know how to solve a problem to solve it; you just need to hammer away until something happens. I'm not sure what this is supposed to have to do with calculus, though : P Solution

Ick.  Well, it's on my list.

I don't wanna...

K, where is has sin(i + 1/2)x and sin(i - 1/2)x, I think they mean sin((i + 1/2)x) and sin((i - 1/2)x), 'cause I can get (a) to work with that.  I got stuck on (b), though, but didn't work on it long.

Hah, I love it when things cancel out. Solution sorry, not up yet

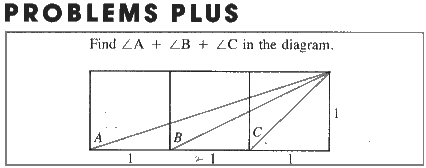
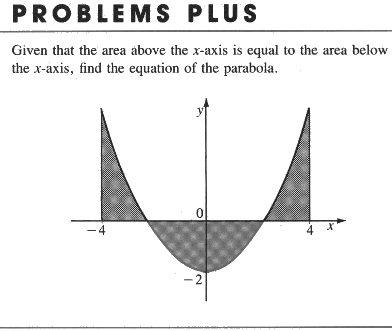
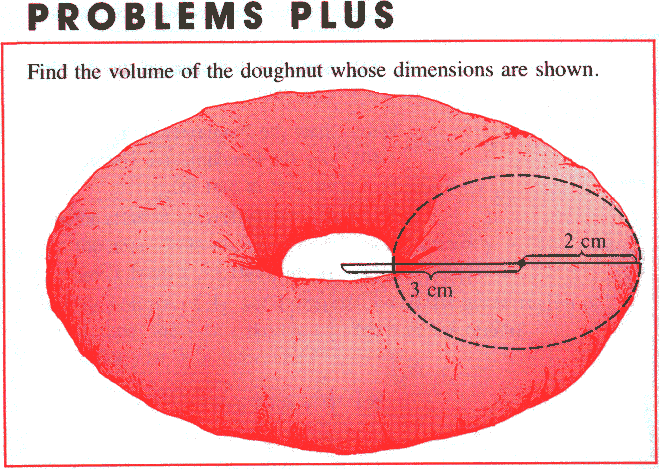
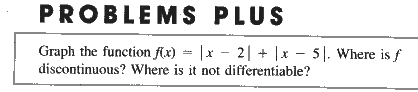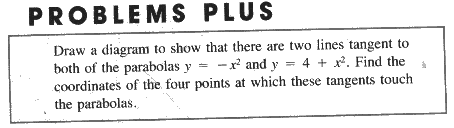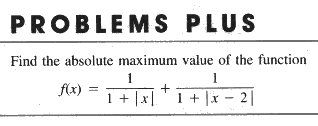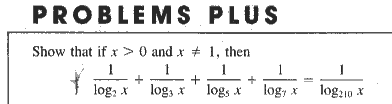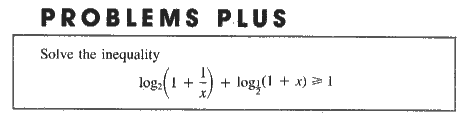My favorite problem!  I was going to show it in all it's 256-colour glory, but the file was too big, so I cut it down this lovely 17-colour image.  I tried 16, but it turned the black into grey...  I have 3 solutions in mind:  easy#1, easy#2, and the hard calculus way involving stuff that I will have to learn how to do since we didn't do it in Calculus last year:  Differentiating Inverse Trigonometric Functions. Hey, grammatical error! Doughnuts, no matter how emotionally attached we may become with them, are not whos, they are whats! Easy#1: Find area of donut cross-section; [ 2^2(pi) ]. Multiply by circumference; [ 2(pi)3 ]. Answer: 24(pi^2) = 236.87 cm^3 of doughnutty goodness. Easy#2: Make the donut into a cylinder. find volume of cylinder; [ 5^2(pi)4 = 100(pi) ]. find volume of cylinder that makes up the hole; [ 1^2(pi)4 = 4(pi) ]. subtract; [ 96(pi) ]. multiply by 1/4(pi), that is, the percentage of area a circle is of a square of the same width(diameter). Answer: 24(pi^2) = 236.87 cm^3 of scrumpdidliumpschiousness. Hard Calculus way (not done yet)

Back
Main