The Theory of Special Relativity
In this paper, I will be describing the
Theory of Special Relativity with simple, logical examples that require only
simple math. I am hoping to explain it
in such a way that anyone reading this paper can learn, and more importantly, understand,
the theory with as little effort as possible.
Before I get into what the consequences of
Special Relativity are, I must first give some background information that led
to the development of the theory.
In the way that sound travels through air
at a constant speed, before Special Relativity was developed it was firmly
believed that light travelled through a medium called the ether at a
constant speed. This ether was
considered to be at absolute rest, and everything in the universe moved through
the ether. In 1887, Albert A. Michelson
and Edward W. Morley performed what is now called the Michelson-Morley
Experiment in which they tried to detect how fast and in what direction the
Earth was moving through the ether.
Without going into the details of how the experiment was done, I'll just
say that they could not detect the presence of the ether at all: it appeared as though the earth was at rest
with the ether. The were many theories
proposed to explain this unexpected result:
notable ones being ether drag, in which objects moving through
the ether drag some of the ether along with it like when you run a knife
through a viscous liquid, which would explain why the Earth did not seem to be
moving with respect to the ether; and George F. Fitzgerald suggested that
objects moving through the ether are contracted, or 'squished' in the
direction of motion. Ether drag was
disproven by some stellar phenomenon, but there was no evidence against
Fitzgerald's suggestion.
Eighteen years later, the Michelson-Morley
Experiment was still being repeated by Morley and others. People must have been convinced that the
ether existed and thought that the experiment was flawed. These experiments still gave the same
results: the Earth was not moving with
respect to the ether. Then, in 1905, an
unknown patent office clerk named Albert Einstein proposed in a paper of his
called "On the Electrodynamics of Moving Bodies" that
·
The laws of physics are the same in all
inertial systems and that no preferred inertial system exists (he called this
The Principle of Relativity), and that
·
The speed of light in a vacuum has the
same value, c, in all inertial systems (The Principle of the Constancy of the
Speed of Light).
Similar
things had been suggested in other papers, but apparently Einstein was unaware
of them. The Special Theory of Relativity is derived from these two
assumptions.
First, I must explain what an inertial
system, also called an inertial frame, is. "Newton's First Law" ("The Law of Inertia"),
states that an object at rest (not moving) will stay at rest unless acted upon
by a force, and that an object in motion will stay in motion (at the same speed
and direction of motion) unless acted upon by a force. If you are in a train moving at a constant
speed and direction, you are in an inertial frame. Being in a car that is moving at a constant speed and direction
is also an inertial frame. There are
also frames called non-inertial frames.
These are frames where objects are being accelerated, such as a car
while it is accelerating. Special
Relativity is only capable of dealing with inertial frames. General Relativity, which took Einstein ten
years to develop after he developed Special Relativity, is used to deal with
the things that go on while an object is under acceleration.
THE LORENTZ TRANSFORMATION
Einstein didn't start relativity from
scratch. In 1895, Hendrik Antoon
Lorentz, in an effort to understand the apparent constancy of the speed of
light, devised a mathematical translation used to translate (change)
co-ordinates from one inertial frame to another. His translation is called The Lorentz Translation. To develop his translation, he started with
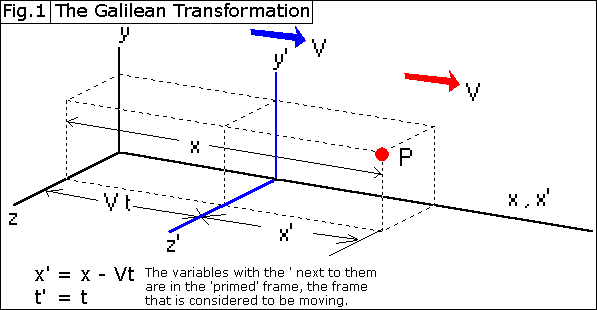
the Galilean Transformation (x' = x - Vt; y' = y;
z' = z; t' = t. See Figure. 1 at the end of this section for
an explanation. In the Galilean
Transformation, time is constant, so time in one frame is the same as time in
any other frame, so t' always would equal t), and tried to make x'² + y'² +
z'² = ct'² (this is the formula for a point on a sphere that is expanding
at the speed of light) translate to x² + y² + z² = ct² because for the
'stationary' frame, light is moving away from it at c, but the same
light is moving away from the 'primed' frame (the one we are considering to be
moving) at the same speed (because c is constant in all inertial frames), so
the light should be at the same distance from both of them. They should both be at the center of the
sphere of light. Using the Galilean
Transformation, x'² + y'² + z'² = t'² would translate to x² - 2xVt
+ V²t² + y² + z² = c²t². He had
to find a new translation for t' = t that would cancel out the -2xVt and
+V²t² terms. Lorentz found that
the correct translation is
![]()
(Notice that if V is is a lot
less than the speed of light, it has almost no effect on the calculation)
Two
variables were then created to make the formulas look simpler:
b(beta) ![]() v/c; g
(gamma)
v/c; g
(gamma) ![]()
![]()
(Notice that g will always be a number greater than 1 if V
is not equal to zero)
Which
made the x' and t' formulas
x' = g(x - bct);
t' = g(t - bx/c)
and
x = g(x' + bct');
t = g(t' + bx'/c)
I am not sure if people paid much
attention to Lorentz's transformation; most were probably still convinced that
there was something wrong with the Michelson-Morley experiment or maybe ether
drag had not been disproven when Lorentz derived his formulas.
Now on to the interesting stuff.
TIME DILATION
The first consequence of the assumption
that the speed of light has the same value in any inertial frame is that time
in different frames must pass at different rates. To an observer, time in frames moving relative to his own frame
appears to be passing at a slower rate than in his own.
Here is an example of why the rate that
time passes at will be different in different frames.
Ignore the math on the right until you
have read the explanation below the picture.
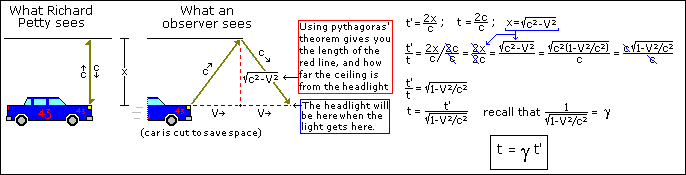
Mr. Petty is racing through a tunnel. His headlights are pointing straight up (he
was in a crash earlier). To Mr. Petty,
the light from his headlight goes straight up at a speed of c, hits the
ceiling, then returns to the headlight at a speed of c. Since time is distance divided by velocity,
the total time that passes from when the light leaves the headlight and returns
is t'=2x/c. Since we are
considering Mr. Petty to be moving, he is in the 'primed' frame, which is why
his t has an apostrophe next to it.
To the observer on the side of the track,
whose frame we are considering to be stationary, the light moves along with the
car, going at a speed of c in a diagonal direction relative to the observer
(the light is always right above the headlight).
We then take a ratio of t' to t (t' / t )
and then substitute their values in.
With some simple grade 10 math and some substituting, we end up with t =
gt'. Since g is always greater than 1 if
V is not zero, time in the primed frame passes at a slower rate than time in
the stationary frame! You may have
noted that the time dilation formula looks different than Lorentz's time
translation, t = g(t' + bx'/c).
This is because when we are measuring time, there is no value for x', so
the +bx'/c term is equal to 0.
There is a slight contradiction here: if there is no preferred inertial frame,
then the 'moving' frame (Richard Petty) would see time going slower in the
'stationary' frame (the observer's).
The problem is that Special Relativity does not apply to non-inertial
frames. When an object is accelerating,
we need to use General Relativity to understand what is going on. The way I see it, the object that actually
gains kinetic energy is the object that the observed effects of Special
Relativity are actually happening to:
when a rocket burns fuel and gains kinetic energy, even though from the
rocket, time in other frames seems to be going slower, it is in fact time in
the rocket that is slowed, not time in the other frames.
Time Dilation has been proven numerous
times in many different experiments.
Particles called pions, which 'live' for only 26ns before
decaying into muons, are found to live many times longer if they are
moving at very high speeds. Also,
highly accurate clocks have been put at the top and bottom of towers and it is
found that the clock at the top of the tower runs slower than the one at the
bottom because the clock at the top moves farther than the other one in the
same amount of time when the Earth rotates.
An interesting thing to note about time
dilation is that if you were going the speed of light, time around you would
not pass, and if you were to go faster than the speed of light, you
would arrive at your destination before you even started your
journey! However, it is impossible to
go the speed of light, and just as impossible to go faster than the speed of
light, as other parts of the theory show.
THE FITZGERALD-LORENTZ CONTRACTION
Fitzgerald was definitely on the right
track when he suggested that objects contract in the direction of their
movement. Length contraction is closely
related to time dilation: the formula
is the opposite of that for time dilation, and with t and t' switched to x and
x': the time dilation formula is t = gt', while the equation for length contraction
that is observed from the stationary frame is x = x'/g.
That is, if someone in a 'stationary' frame takes a measurement of a
length in a moving frame, he will get a smaller measurement than would someone
who is in the moving frame because if g
is greater than one, then the x measurement will be smaller than x'
measurement.
For example, I have two 3m long boxes that
each have a lamp at one end. Light
takes 10 nanoseconds to travel 3m, so if I turn on the lamp in one of the
boxes, it will take 10ns for the light to hit the other side of the box. I put one of the boxes on a rocket ship and
now the box is moving at a velocity of 0.6c relative to me. Both lamps turn on at the same time t=t'=0. i observe the light to leave the lamp in
each of the boxes at the same time, and the light hits the other end of the
boxes at the same time in my frame. In
the box in my frame, the light takes 10ns to go from one side to the
other. Use the time dilation formula
(t=gt') to find out how long the
light takes to go from one end of the box in the moving frame to the other end.
t = 10ns; V = 0.6c;
g = 1/sqrt(1 - v²/c²)
t = gt'
10ns = t' (1/sqrt(1 -
v²/c²))
10ns = t' / sqrt(1 -
(0.6c)²/c²)
10ns = t' / sqrt(1-0.36)
10ns = t' / sqrt(0.64)
10ns = t' / 0.8
t' = 8ns
So,
if only 8ns has passed in the moving box and light went from one end to the
other, the box can not be 3m long! The
moving box must only be 0.8 x 3m = 2.4m long!
Of course, a person in the box would still
measure the box to be 3m long and he would measure the time to be 10ns. The confusing thing here is that in Special
Relativity, what is observed is not necessarily what has happened. If I am stationary, and the two boxes are
moving away from me at the same speed, but in opposite directions, then I would
observe time to slow down the same rate in both of the boxes, and I would say
that both boxes has contracted equally; however, someone in one of the boxes
would look at the other box and say that time is going slower in that box than
in his own box and the other box is also shorter than his box! Again, this problem can only be solved using
non-inertial frames and General Relativity.
Another problem that I had here that
confused me was that though the Lorentz translations for x and t were nearly identical
( x = g(x' + bct'); t = g(t' + bx'/c) ), the equations I derived
for x and t using these examples were opposites, dividing in one and
multiplying in the other: x = x'/g; t =
gt' ! What I didn't realize was that when I was
measuring t, I was measuring something that is in my own frame, but my x was
measuring the length of the box that is in the moving frame! So x is actually a measurement of x' and x'
is a measurement of x.
An interesting thing that I noted about
this formula is that if you are going the speed of light, the term on the
bottom of the equation, sqrt(1 - v²/c²), would give a zero, resulting in
division by zero, which is an impossibility!
If the faster you go, the more contracted you got, you could extrapolate
that if you managed to reach the speed of light, you would be contracted into
nothingness! This is just one of the
formulas of Special Relativity that shows that it is impossible to reach the
speed of light.
VELOCITY TRANSLATION
I often used to wonder why it was not
possible to get something going the speed of light by firing it from an object
that was already moving at a very high speed.
The reason is that if space is contracted in the moving frame, then if
you fired something from that frame at a certain velocity, it would not be
going as fast relative to the stationary frame! The formula for translating velocities that are relative a frame
that is considered to be moving is
Vo = (V + v') / (1
+ Vv'/c²)
Vo is the velocity relative the
stationary frame of the object being fired from an already moving frame, V
is the velocity of the moving frame relative the stationary frame, and v' is
the velocity of the object in question in the primed frame.
This formula also makes reaching the speed
of light an impossiblity: if V or V' is
less than c, then Vo will be less than c, and if
one of the velocities is c, no matter how high the other velocity is, Vo will be only c.
MASS INCREASE WITH VELOCITY
Special Relativity predicted that the
faster an object moves, the more its mass will be. Two formulas are needed to explain why this happens: the first is the Velocity Translation (Vo = (v' + V) /
(1
+ v'V/c²))
and the second is
P = mV
This
is the formula for force (P = force).
The faster on object is moving, the more force it will have; also the
heavier an object is, the more force it will have when moving.
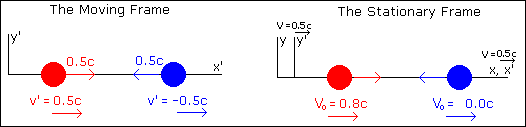
For this example, we have 2
velcro-balls. One is blue, the other
red. Both balls weigh the same thing
when at rest (mo1 = mo2. The o denotes that the mass is
measured when the object is at rest).
When these balls collide, they stick together.
In the moving frame, the balls are moving
toward each other each with the same velocity, v' = 0.5c. When they collide in the moving frame, their
forces are equal (because both their velocities are equal, and even though
velocity does affect their masses, since the velocities are the same, their
masses would still be the same), so they stick together and stop moving
relative to the moving frame. The
moving frame, however, is moving away from the stationary frame at 0.5c, which
means the balls are moving at 0.5c in relation to the stationary frame, too.
Now we will look at this collision from
the view point of someone in the stationary frame.
Use the velocity translation to translate
their velocities from the moving frame to the stationary frame. We find that the red ball is moving at
Vo = (V + v') / (1
+ Vv'/c²)
Vo = (0.5c + 0.5c) / (1
+ (0.5c)(0.5c)/c²)
Vo = (c) / (1
+ 0.25c²/c²)
Vo = 0.8c
and
that the blue ball is moving at
Vo = (0.5c - 0.5c) / (1
+ (0.5c)(0.5c)/c²)
Vo = (0.0c) / (1
+ (0.25c²/c²)
Vo = 0.0c
So,
in the stationary frame, the red ball has a force of
Pred = mv
Pred = m1 0.8c
and
the blue one has a force of
Pblue = mv
Pblue = m2 0.0c
The
balls collide and stick together. Their
collective mass is now M = m1
+ m2. Since the blue ball is not moving, it's mass is its rest mass, mo., so the total mass becomes
m1 + mo. Their total force is now P = Pblue + Pred
= m1 0.8c + m2 0.0c = m1 0.8c. Using the force equation, we can now solve
for the mass of the red ball (the blue ball is at rest relative to our frame,
so we know that it's mass has not changed).
P=MV
m1 0.8c = m1 + mo(0.5c)
m1 1.6 = m1 + mo
m1 1.6 - m1= mo
m1 0.6 = mo
m1 = mo/0.6 !
Remembering
that the original velocity of m1
in the stationary frame was 0.8c, if we put 0.8c into g, we get 1/0.6, so the formula for the mass
of a moving object is m = gmo, since mo/0.6 is the same as mo(1/0.6). Using different velocities, you would find
that this is the proper formula.
It is not hard to verify mass increase
experimentally. One just takes a
particle at rest, measures its mass, then fires it at a high velocity at a
surface that records how much force the particle hit with. If the force is greater than moV by the same amount
predicted by the theory, then the theory is correct. Indeed, this has been verified.
This is another equation that limits
objects to speeds under the speed of light.
The faster that you go, the smaller the denominator of the equation
becomes, and the higher the mass becomes, and since more massive objects
require more energy accelerate them, eventually you would find that you needed
an infinite amount of energy to make the leap to the speed of light.
THE EQUIVALENCE OF ENERGY AND MASS
The most famous equation in the world is
E=mc². There is a good reason that this
is a famous equation: it revolutionized
the world by bringing about the idea of using small amounts of matter to create
huge amounts of energy. Since c² is a
huge number (9.00 x 10^16 m²/s²!), this means that a very small amount of mass
is actually a huge amount of energy.
In our last section, we proved that the
faster and object moves, the more it weighs.
And what is velocity but a manifestation of energy? It takes energy to speed something up. When an object is accelerated, it gains
kinetic energy in the form of movement, velocity. It also gains mass proportionally to how much much velocity
energy it has, as was shown in the previous section.
In the formula, we know what m is, it a
measurement of mass in kilograms (kg), and we know that c is the distant, in
metres, that light travels in a second.
So the unit for energy is mc² = kg m²/s². The m in this unit is a measurement in metres, not of mass, in
this case. Using any old physics text
book, you can find that this unit, kg m²/s², is called a joule (J).
Einstein is reported to have said that
there is enough energy in one matchstick to melt all the snow in
Switzerland. Using the formula, we can
figure out how much energy it suppsedly would take to melt Switzerland's snow.
A match weighs about 1.00g,
which is 0.00100kg, or 1.00 x 10^-3kg.
E = mc²
E = 1.00 x 10^-3kg (3.00 x
10^8 m/s)²
E = 1.00 x 10^-3kg (9.00 x
10^16 m²/s²)
E = 9.00 x 10^13 kg m²/s²
E = 9.00 x 10^13 J
That is a lot of energy!
In fact, the average person puts out
roughly 2 x 10^11 J of energy in their entire lifetime, and the amount of
energy in that little matchstick is 450 times this amount!
CONCLUSION
After learning Special Relativity
something becomes very apparent:
Einstein's genius was not necessarily in math, but in logic and
imagination. After all, there was no
math in the theory that a grade 10 student could not do. The hard part, the part that Einstein was
able to do and no one else, was taking the results from one situation and
applying them to a new, different situation.
Einstein was able to see things that no one else had ever thought to
look for. It is his type of thought
that everyone should strive toward.